Semi-major axis change Change of Binary Parameters: Change of Binary Parameters:

Mass change

The mass of the star that loses matter is

Accordingly, the mass of the accreting star is

where is the accretion rate  of the captured matter.

For stages with no RL overflow, the accretion rate of the captured stellar wind matter is

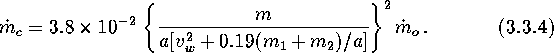
At stages with RL overflow and both normal stars we will assume a mildly non-conservative mass transfer

This means that the evolution cannot be fully conservative as a rule, since during the first mass transfer episode the more massive star is usually characterized by a shorter thermal time-scale.  

In the case of compact accretors, we require the rate of their mass increase to be limited by the accretion energy output equal to the critical Eddington luminosity 

( is the Thompson cross-section) reached at the stopping radius  for the accreted matter (see detailed discussion in Lipunov (1992)[107]), which corresponds to a critical accretion  rate

Thus, the mass of the accreting compact star at the end of the stage is determined by the relation