At first we shall estimate D, using eq. (6). In this equation all variables, except , are known (in principle). Their values taken from Lipunov (1992) are shown in table 1.
Nagase (1992) gives results of GINGA observations of the cyclotron lines in X-ray pulsars. For Vela X-1 and Her X-1 values of magnetic field, B, coincides with the values that we used when radii of NS's are and correspondently. The value for B obtained from observations for Vela X-1, , coincides quite well with the assumption that there is no stable accretion disk in this pulsar.
Characteristic time for the wind-accreting systems can be determined from the equation:
where - a fraction of the specific angular momentum of
the Kepler orbit at the magnitospheric radius, A-noise level (see table 2)
(de Kool 
Anzer 1993).
In eq.(6) for we must use minimum values. These times were calculated using equations for pure spin-up from Lipunov (1992), are shown in table 1.
We took
From eq. (7) we can get
for Vela X-1 and GX 301-2. For Her X-1 and Cen X-3,
is determined from the graph in de Kool Anzer (1993)
(see table 3).
So we can write equation for D in the form:
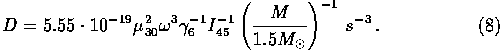
Values of D for four systems are shown in table 3.
From the theory of diffusion we can write:
where is the characteristic length in the frequency space.
For characteristic time in this space we can write:
We can give a physical interpretation for for wind-fed pulsars as a characteristic time of the momentum transfer:
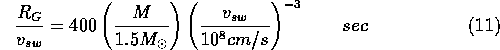
For we obtain and for we obtain . These velocities are close to obtained using estimates of the 'diffusion coefficient'.
These characteristic time scales are also shown in table 3.
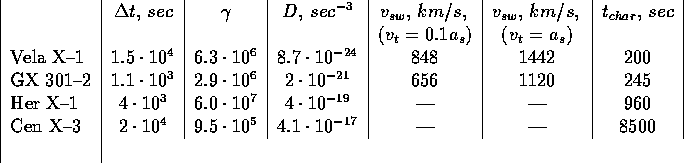
Table 3: