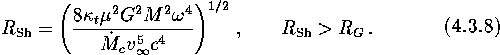The Stopping Radius in ``Ecology'' of Magnetic Rotators The Environment of the

The Stopping Radius

    

Now we consider qualitatively the effect of the electromagnetic field of a magnetic rotator on the accreting plasma. Consider a magnetic rotator with a dipole magnetic moment , rotational frequency and mass M. At distances the surrounding plasma is characterized by the following parameters: density , sound velocity and/or velocity relative to the star. The plasma will tend to accrete on to the star under the action of gravitation. The electromagnetic field, however, will obstruct this process, and the accreting matter will come to a stop at a certain distance.

Basically, two different cases can be considered: (1) when the interaction takes place beyond the light cylinder, , and (2) the accreting plasma penetrates the light cylinder .

(1) Case (1) was first considered by Schwartzman (1970b,c)[175, 174]. In this case the magnetic rotator generates a relativistic wind consisting of a flux of different kinds of electromagnetic waves and relativistic particles. The form in which the major part of the rotational energy of the star is ejected is not important at this stage. What is important is that both relativistic particles and magnetic dipole radiation will transfer their momentum and hence exert pressure on the accreting plasma. Indeed, random magnetic fields are always present in the accreting plasma. The Larmor radius of a particle with energy  eV moving in the lowest interstellar magnetic field  G is much smaller than the characteristic values of radius of interaction, so the relativistic wind will be trapped by the magnetic field of the accreting plasma and thus will transfer its momentum to it.

Thus, a relativistic wind can effectively impede the accretion of matter. A cavern is formed around the magnetic rotator,   and the pressure of the ejected wind at its boundary balances the ram pressure of the accreting plasma :

This equality defines a characteristic size of the stopping radius, which we call the Schwartzman radius  .

(2) The pressure of the accreting plasma is high enough to permit the plasma to enter the light cylinder . Since the magnetic field inside the light cylinder decreases as a dipole field, the magnetic pressure is given by

Matching this pressure to the ram pressure of the accreting plasma yields the Alfvén radius  .

The magnetic pressure and the pressure of the relativistic wind can be written in the following convenient form:

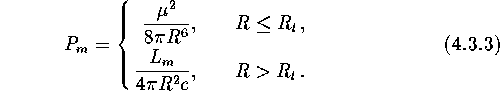
We introduce a dimensionless factor such that the power of the ejected wind is

Assuming , we get for a continuous function whose qualitative behavior is shown in Figure 4.

 
Figure 4: Internal and external pressure laws.   

The accreting pressure of plasma outside the capture radius  is nearly constant, and hence gravitation does not affect the medium parameters significantly. In contrast, at distances inside the gravitational capture radius the matter falls almost freely and exerts pressure on the ``wall'' equal to the dynamical pressure. For spherically symmetric accretion   we obtain

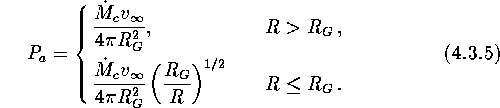
Here we used the continuity equation . When presented in this form, the pressure is a continuous function of distance (Figure 4).

Summarizing, for the stopping radius  we get

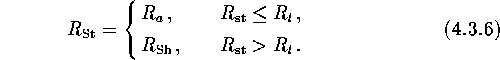
The expressions for the Alfvén radius  are:

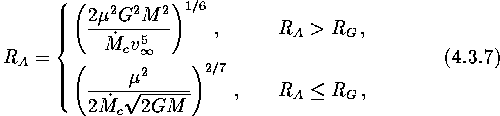
and for the Schwartzman radius: 

The Stopping Radius in ``Ecology'' of Magnetic Rotators The Environment of the