Next: Phenomenological Kick Velocity Up: Restrictions on the Scenario Previous: The COOC Criterion (Criterion
Next: Phenomenological
Kick Velocity Up: Restrictions
on the Scenario Previous: The
COOC Criterion (Criterion
Each run of our calculations consisted of computing 
evolutionary tracks for 10 equal intervals of the initial mass ratio 
=(0-0.1, 0.1-0.2, ..., 0.9-1.0) performed for seven values of the common
envelope efficiency 
, 0.3, 0.5, 1, 2, 3, 10 and 10 values of the kick velocity 0, 25, 50, 100,
200, 300, 400, 500, 700, 1000 km s
. In total, we obtained 700 matrices of stages. Then, for each value of
the 
and w we convolved the matrices from different intervals of mass
ratio according to the trial initial mass ratio distribution for 50 values
of the exponent 
ranging from 0 to 5 (that is, from a flat to a highly peaked toward unity
initial distribution). Further, we convolved the matrices for the specified
initial power law for the assumed kick velocity distribution (see the next
section).
In our calculations we prohibited accretion-induced collapse (AIC) of accreting WD, as otherwise we would get an excessive number of long-lived low-mass X-ray sources which would give an unobservably high X-ray luminosity of the Galaxy. However, we must note that the question of the AIC possibility for massive O-Ne-Mg WD deserves more detailed study. Here we only note that observational evidence favoring the AIC constantly appear in literature (e.g. Lipunov and Postnov (1985)[111]).
The results of testing
and
parameters without kick velocity are presented in the form of "topographical
maps" (i.e. as isolines) of constant ``COOC'' criterion in the 
plane calculated separately for each of the binary species listed in Table 4
(Figures 16-20).
The total COOC criterion calculated with equal weights 
is shown in Figure 21.
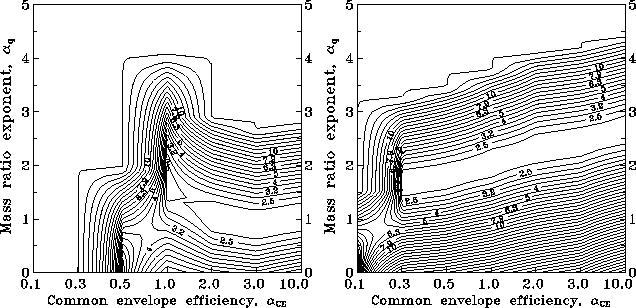
Figure 17: The same as shown in Figure 16
for the number of accreting NS with Be-stars.
Figure 16: The COOC criterion for the total X-ray luminosity of
LMXB assuming no kick.
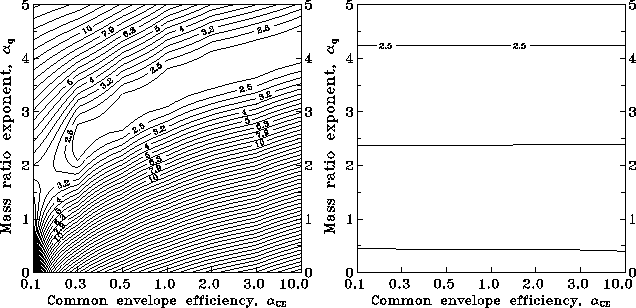
Figure 19: The same as shown in Figure 16
for the number of BH with massive OB-stars (Cyg X-1 like binaries).
Figure 18: The same as shown in Figure 16
for the number of X-ray pulsars with OB-stars.
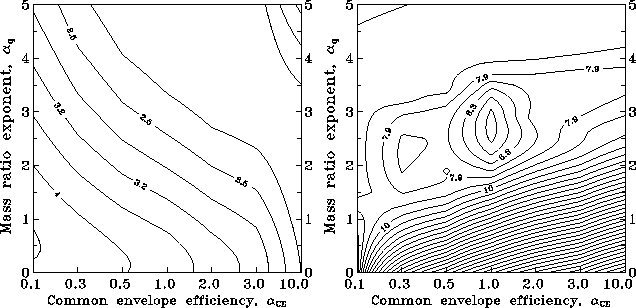
Figure: The same as shown in Figure 16
for all the species from Table 4.
Figure 20: The same as shown in Figure 16
for the number of cataclysmic variables.
It is clear from these figures that the best coincidence with the observations
is reached when 
-3 and 
-10. A rather weak influence of the common
envelope efficiency is connected with a wide log-normal
distribution of binaries by initial semimajor axes, so only boundary effects
(corresponding to the extreme values of
) can change the results significantly.
As for the initial binary mass ratio distribution, it seems that at least for those binaries that produce NS during the course of their evolution, it must peak rather strongly toward unity, which is opposite to the widely used flat-like distributions (see, van den Heuvel, 1994[205]); however, high mass ratios among massive unevolved binary O-stars appear to occur less frequently, thus confirming our conclusions (Garmany et al., 1980[54]).
In Figure 22 we show how the total
accretion X-ray luminosity of the LMXB depends on the parameter
for different values of the parameter
. It is worth noting that for 
the luminosity is essentially independent of the collapse anisotropy
and can be analytically fitted by the power law
for a 
spiral galaxy with a constant star formation rate.
Figure 22: Total X-ray luminosity of the galactic LMXB as a function
of
for different common envelope efficiencies
without kick.
