Next: X-ray Galactic Sources and Up: Restrictions on the Scenario Previous: The Effect of Kick
Next: X-ray
Galactic Sources and Up: Restrictions
on the Scenario Previous: The
Effect of Kick
We assumed that in the artificial galaxy we modeled the number of single
stars is equal to the number of stars entering binaries. The calculations
were done for the initial mass ratio power 
ranging from 0 to 2.
Figure 23: Binary pulsar fractions among the total number of
pulsars as a function of the mean kick velocity for
a maxwellian distribution (left-hand panel) and that
fitting Lyne and Lorimer's data (right-hand panel). The width of each curve
reflects the dispersion of power index 
in the initial mass ratio spectrum. The number for pulsars+planets
is reduced 10 times for clarity.
Figure 23 (left-hand panel) shows
the dependence of the fraction of different types of binary pulsars among
the total number of radiopulsars (including those produced by single massive
stars) on the mean maxwellian kick velocity 
(three-dimensional). For completeness, we added the computed number of
PSR+BH binaries (assuming a critical mass of the pre-collapsing star of
and the mass fraction forming the BH of 0.3; see Lipunov et al.,
(1994b)[124]).
The upper axis shows the mean transverse recoil velocity of pulsars
corresponding to the assumed
. The right-hand panel shows the same curves obtained for the kick velocity
distribution [equation (7.4.2)] fitting
the pulsars' transverse velocity distribution given by Lyne and Lorimer
(1994)[132]. As expected, increasing
the mean kick velocity decreases all binary pulsar fractions. In
this figure, the fraction of pulsars with planets (PSR+PL) is reduced by
a factor of 10 for clarity.
The non-monotonic character of the PSR+PL curve is explained by the fact that in the general case a small kick velocity reduces the new periastron of the binary system making dissipative processes more efficient, which leads to WD Roche lobe overflow with subsequent planet formation. A more rapid decline for the PSR+NS and PSR+BH systems is caused by the system's undergoing two collapses (and hence, two kicks), and thus these binaries are subjected to the danger of disruption twice as much.
Obviously, the ``maxwellian'' curves decreases faster (left-hand panel
of Figure 23) than the ``Land L'' ones.
This is due to the flat power-law asymptotics of Lyne and Lorimer's two-dimensional
distribution at low velocities. Indeed, for large mean
kick velocities the maxwellian distribution has an
asymptotic behavior like 
in the crucial region of slow velocities ( 
300 km s
) which are less or comparable with a characteristic binary orbital velocity,
whereas 
is much flatter. We also note that analogous calculations for the delta-function-like
kick velocity distribution (not shown in these figures) naturally lead
to an even faster decrease of the binary radiopulsar fractions.
Figure: The COOC criterion for binary radiopulsar species from
Table 4 as a function of the mean kick velocity.
Figure 24 shows the COOC criterion
(equation 7.2.1) taken over PSR+
[2]OB, PSR+NS and PSR+WD systems (PSR+PL were excluded because there could
be other ways such systems formed that are not accounted for by our code
as yet) as a function of mean kick velocity. It is clearly seen from this
figure that the combined calculated and observed numbers differ by less
than three times for the mean kick velocities 
km s
, with the minimum (COOC 
2.3) at
75-100 km s
.
Let us turn now to a two-dimensional distribution of the pulsars' transverse
velocities which are really observed (Lyne and Lorimer, 1994[132];
Frail et al., 1994[53]). As
mentioned above, it is well reproduced by the distribution given by equation
(7.4.2) with 
km s
,
which corresponds to the mean velocity 
km s
(we note that the mean recoil space velocity of pulsars subjected to such
kick distribution is
370 km s
; obviously, for high velocities kick and recoil should be the same). This
mean kick velocity corresponds to COOC 
5 (Figure 24), that is to a fivefold
disagreement with the observed situation. The higher mean recoil transverse
velocities reported by Frail et al., (1994)[53],
500-1000 km s
, would give a more dramatic inconsistency. Figure 23
clearly demonstrates that for high mean space velocities >300 km s
the observed binary pulsars ``Zoo'' would rapidly vanish.
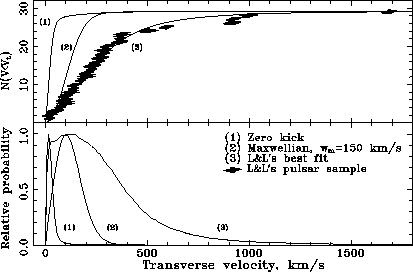
Figure 25: The simulated pulsar transverse velocity distribution
(bottom panel) and cumulative distribution (upper panel) for different
kicks. The dots are the observed distribution from Lyne and Lorimer (1994).[132]
In Figure 25 we present the calculated
pulsars' transverse recoil velocity distribution for three specific cases:
with zero kick (curve (1)), the maxwellian kick with 
km s
(curve (2)) and the distribution (3) giving the best fit to Lyne and Lorimer's
data (shown by filled circles). The cumulative distribution is shown for
comparison (upper panel).
The calculations presented above clearly demonstrate a strong decrease in number of binary pulsars with diverse secondary components on the assumed kick velocity the NS acquires at birth. On the other hand, high birth velocities for pulsars seem to be really observed (Lyne and Lorimer, 1994[132]; Frail et al, 1994[53]). Thus, a paradoxical situation emerges: we have to make a choice between the high birth space velocities for the pulsars and the observed reach ``Zoo'' of binary pulsars in the galactic disk! Putting aside a thorough analysis of the observational data (which could well be influenced by a number of selection effects leading to an underestimation of low-velocity pulsars; e.g. Tutukov et al., 1984[198]), a possible cause could be the slow steady acceleration of NS which would not disrupt the binary system, but would impart a high space velocity for single pulsars (for example, the rocket mechanism suggested by Tademary and Harrison (1975)[185] caused by an asymmetric pulsar's emission). The recently reported one-sided X-ray jet from the Vela pulsar (Markwardt and Ögelman, 1995)[136] may provide fresh support for this idea.
What to do with the fast pulsars moving with velocities >1000 km
s
? The highest pulsar velocities resulting from the disruption of a NS -
massive helium star binary during
a spherically-symmetric collapse of the helium star cannot be greater than
700-800 km s
. The mechanism recently suggested by Bisnovatyi-Kogan (1993)[14]
allows one to obtain pulsar birth velocities as high as 3000 km s
, but still requires a very strong magnetic field ( 
G) at birth. Imshennik's (1992)[77]
mechanism of double NS formation during the collapse with subsequent Roche
lobe overflow of the less massive NS and its explosion after a minimum
mass of about 
has been reached, although not requiring such a high magnetic field,
could lead to very high individual space velocities, but hardly to the
high mean kicks required to fit the observations.
Therefore, the observed diversity and number of binary pulsars, while
requiring a small kick velocity ( 
100-150 km
s)
to be present, are, at the same time, in strong contradiction with the
presently derived high mean transverse velocities of pulsars.
