Next: Effect of sources evolution Up: Evolution of the Double Previous: Evolution of the Double
Next: Effect
of sources evolution Up: Evolution
of the Double Previous: Evolution
of the Double
It is reasonable to expect a priori that the evolution of events is
strongly time dependent, so the star formation history 
in a galaxy is another important parameter. Therefore, by calculating the
evolution of events after a 
-function like star formation burst, one gets a Green
function 
for any
arbitrary star formation history.
At the one extreme we assume instantaneous star formation at a particular
redshift resulting in a stellar system which we call ``elliptical''
since stars in elliptical galaxies to a good approximation can be assumed
to be old and little if any additional star formation is occuring today.
Thus the event rates in ``ellipticals'' can be described by the computed
Green function. At the other extreme, constant star formation (
= const) would result in ``spiral''-like stellar systems.
Irregular galaxies have probably also an irregular star formation history,
but their contribution to the overall event rate hardly exceeds their fraction
among all galaxies, that is 5-7 percent, so we neglect them in this context.
The source evolution in a galaxy with given star formation rate
is thus calculated as
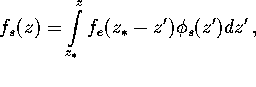
where 
is the redshift at the turn-on of star formation, which is the second important
parameter of the model. Assuming to the zero approximation 
= const, we get
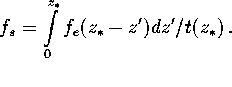
We parametrize the star formation history in the Universe by the fractional
part of the luminous baryonic matter entering into elliptical galaxies,
, where E
and S refer to ``elliptical'' galaxies (i.e.
without additional star formation) and ``spiral'' galaxies
(with a constant star formation rate). In fact, this parameter must be
higher than the presently observed fraction of elliptical galaxies, as
any galaxy must have had more violent star formation at earlier time. The
galaxies are supposed to be formed at the moment
with the initial star formation during first 500 Myr. The mean number of
galaxies each of 
was taken 
Mpc
(this roughly corresponds to a density of baryonic matter in galaxies without
hidden mass of 
).
We make usual assumptions about initial distributions of binary stars
(see Section 6) similar to those
presently observed in our Galaxy (a Salpeter function for mass 
of the primary component, 
and a flat distribution of the initial binary separations A: 
). Based on findings by the Scenario Machine analysis of the evolutionary
scenario by Lipunov et al. (1995b)[128]
(Section 7), we take the initial
mass ratio distribution in a power-law form 
and the efficiency coefficient of angular momentum removal at the common
envelope stage 
(as defined by van den Heuvel 1994[205]).